Beschreibung
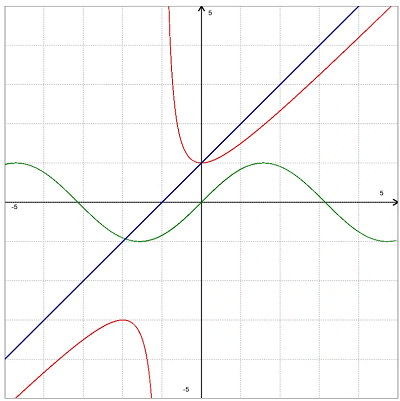
Auf der Seite dieses Funktionsplotters können Sie zur Darstellung in der Zwei-Dimensionalen-Ebene die Graphen von Mathematischen Funktionen betrachten. Sie können gleichzeitig drei Funktionen überlagert im Funktionsplotter anzeigen lassen und diese dadurch vergleichen. Weiterhin können Sie die 1. und 2. Ableitung bestimmen lassen. Damit kann man gut die Bedeutung der ersten und 2. Ableitung analysieren.
Wenn Sie mögen, können Sie den Graphen des Funktionsplotters auch als Bild auf der Festplatte abspeichern.
Folgende Funktionen können dargestellt werden
Jede Funktion
- Prinzipiell kann jede Zwei-Dimensionelle Funktion dargestellt werden!
- Probieren Sie es aus: Funktion
Trigonometrische Funktionen
Hyperbolicus-Funktionen
Wurzelfunktionen
Logaritmus-Funktionen
Polynom-Funktionen
Sonstige Funktionen
Außerdem hat man diverse Möglichkeiten Parameter anzupasen, wie auch die Plotterfläche des Funktionsplotters. Klicken Sie auf das blaue Viereck, und es öffnet sich ein Dialog.
Diese Seite ist auch Responsive - die Seite ist daher auch für kleinere Bildschirme optimiert. Aber schauen Sie doch gerne selber und öffnen Sie die Site des Funktionsplotters auf Ihrem Smartphone.
CLOSE
Betrags-Funktion
In der Mathematik ordnet die Betragsfunktion einer reellen oder komplexen Zahl ihren Abstand zur Null zu. Dieser sogenannte absolute Betrag, Absolutbetrag, Absolutwert oder auch schlicht Betrag ist immer eine nichtnegative reelle Zahl. Der Betrag einer Zahl x wird meist mit | x |, seltener mit abs ( x ), bezeichnet. Das Quadrat der Betragsfunktion wird auch Betragsquadrat genannt.
Arcus-Cosinus-Funktion
Arkuskosinus (oder auch Arkuscosinus) – geschrieben arccos oder acos – sind Umkehrfunktionen der (geeignet) eingeschränkten Kosinusfunktion. Kosinus ist eine Funktion, die einen Winkel auf einen Wert im Intervall [ − 1 , 1 ] abbildet; als deren Umkehrfunktion bildet Arkuskosinus einen Wert aus [ − 1 , 1 ] wieder auf einen zugehörigen Winkel ab. Da der Kosinus eine periodische Funktion ist, gibt es aber zu jedem Wert aus [ − 1 , 1 ] unendlich viele zugehörige Winkel. Daher wird zur Umkehrung von Kosinus dessen Definitionsbereich auf [ 0 , π ] für Kosinus eingeschränkt. Kosinus ist auf diesen Intervallen streng monoton und daher umkehrbar.
Zusammen mit dem Arkustangens als Umkehrfunktion des (natürlich ebenfalls geeignet eingeschränkten) Tangens bildet der Arkuskosinus den Kern der Klasse der Arkusfunktionen. Aufgrund der in neuerer Zeit für Umkehrfunktionen gebräuchlichen Schreibweise f − 1 beginnen die namentlich auf Taschenrechnern verbreiteten Schreibweisen sin − 1 die klassische Schreibweise arccos zu verdrängen, was eventuell zu Verwechslungen mit den Kehrwert Kosinus (Kosekans und Sekans) führen kann.
Areakosinus hyperbolicus-Funktion
Der Areakosinus Hyperbolicus (abgekürzt arcosh oder acosh) gehört zu den Areafunktionen und ist die Umkehrfunktion vom Kosinus Hyperbolicus.
Arcuskotangens-Funktion
Der Arkuskotangens ist mit dem Arkustangens eine miteinander verwandte mathematische Arkusfunktion. Sie ist die Umkehrfunktionen der geeignet eingeschränkten Kotangensfunktionen: Eine Einschränkung der ursprünglichen Definitionsbereiche ist nötig, weil Kotangens eine periodische Funktion ist. Man wählt beim Kotangens das Intervall ] 0 , π [
Neben mit Arkussinus und Arkuskosinus als Umkehrfunktionen des Sinus und Kosinus bildet der Arkustangens den Kern der Klasse der Arkusfunktionen. Zusammen mit den Areafunktionen sind sie in der komplexen Funktionentheorie Abwandlungen des komplexen Logarithmus, von dem sie auch die "Mehrdeutigkeit" erben, die ihrerseits von der Periodizität der komplexen Exponentialfunktion herrührt.
Area Kotangens hyperbolicus-Funktion
Area Kotangens Hyperbolicus ist die Umkehrfunktion von Kotangens hyperbolicus und damit eine Area-Funktion.
Arkussinus-Funktion
Der Arkussinus – geschrieben arcsin oder asin – ist die Umkehrfunktion der (geeignet) eingeschränkten Sinusfunktion. Sinus ist eine Funktion, die einen Winkel auf einen Wert im Intervall [ − 1 , 1 ] abbildet; als deren Umkehrfunktion bilde Arkussinus einen Wert aus [ − 1 , 1 ] wieder auf einen zugehörigen Winkel ab. Da Sinus eine periodische Funktion ist, gibt es aber zu jedem Wert aus [ − 1 , 1 ] unendlich viele zugehörige Winkel. Daher wird zur Umkehrung von Sinus dessen Definitionsbereich auf das Intervall [ − π 2 , π 2 ] für Sinus ueingeschränkt. Sinus ist auf diesen Intervallen streng monoton und daher umkehrbar.
Zusammen mit dem Arkustangens als Umkehrfunktion des (natürlich ebenfalls geeignet eingeschränkten) Tangens bilden der Arkussinus und Arkuskosinus den Kern der Klasse der Arkusfunktionen. Aufgrund der in neuerer Zeit für Umkehrfunktionen gebräuchlichen Schreibweise f − 1 beginnen die namentlich auf Taschenrechnern verbreiteten Schreibweisen sin − 1 die klassische Schreibweise arcsin bzw. arccos zu verdrängen, was eventuell zu Verwechslungen mit den Kehrwerten des Sinus und Kosinus (Kosekans und Sekans) führen kann.
Areasinus hyperbolicus-Funktion
Areasinus hyperbolicus (abgekürzt arsinh oder asinh ) gehört zu den Areafunktionen und ist die Umkehrfunktion vom Sinus hyperbolicus.
Arcustangens-Funktion
Arkustangens ist eine mathematische Arkusfunktion. Sie ist die Umkehrfunktionen der geeignet eingeschränkten Tangensfunktion: Eine Einschränkung der ursprünglichen Definitionsbereiche ist nötig, weil Tangens eine periodische Funktion ist. Man wählt beim Tangens das Intervall ] − π / 2 , π / 2
Zusammen mit Arkussinus und Arkuskosinus als Umkehrfunktionen des Sinus und Kosinus bildet der Arkustangens den Kern der Klasse der Arkusfunktionen. Zusammen mit den Areafunktionen sind sie in der komplexen Funktionentheorie Abwandlungen des komplexen Logarithmus, von dem sie auch die "Mehrdeutigkeit" erben, die ihrerseits von der Periodizität der komplexen Exponentialfunktion herrührt.
Areatangens hyperbolicus-Funktion
Areatangens hyperbolicus ist die Umkehrfunktionen von Tangens hyperbolicus und damit eine Area-Funktion.
Cosinus-Funktion
Die Cosinus-Funktion ist neben der Sinus-Funktion eine elementare mathematische Funktion. Vor Tangens und Kotangens, Sekans und Kosekans bildet sie die wichtigste trigonometrischen Funktion. Cosinus wird unter anderem in der Geometrie für Dreiecksberechnungen in der ebenen und sphärischen Trigonometrie benötigt. Auch in der Analysis ist sie wichtig.
Wellen wie Schallwellen, Wasserwellen und elektromagnetische Wellen lassen sich als aus Cosinuswellen zusammengesetzt beschreiben, sodass die Funktion auch in der Physik als harmonische Schwingung allgegenwärtig sind.
Cosinus hyperbolicus-Funktion
Der Cosinus hyperbolicus ist eine mathematische Hyperbelfunktion, auch Hyperbelcosinus genannt; sie trägt die Symbole cosh. Der Cosinus hyperbolicus beschreibt unter anderem den Verlauf eines an zwei Punkten aufgehängten Seils. Sein Graph wird deshalb auch als Katenoide (Kettenlinie) bezeichnet.
Cotangens-Funktion
Cotangens ist eine trigonometrische Funktion und spielt in der Mathematik und ihren Anwendungsgebieten eine herausragende Rolle. Der Kotangens des Winkels x mit cot x. In älterer Literatur findet man auch die Schreibweisen ctg x für den Kotangens.
Cotangens hyperbolicus-Funktion
Kotangens hyperbolicus ist eine Hyperbelfunktion. Man nennt sie auch Hyperbelkotangens oder hyperbolischen Kotangens.
Kosekans-Funktion
Kosekans ist eine trigonometrische Funktion. Der Kosekans wird mit csc ( x ) oder cosec ( x ) bezeichnet. Die Funktionen hat ihren Namen durch die Definition im Einheitskreis. Die Funktionswerte entsprechen der Länge von Sekantenabschnitten.Im rechtwinkligen Dreieck ist der Kosekans das Verhältnis der Hypotenuse zur Gegenkathete und damit die Kehrwert-Funktion der Sinusfunktion.
Exponentialfunktion
In der Mathematik bezeichnet man als Exponentialfunktion eine Funktion der Form a^x mit einer reellen Zahl a > 0 und a ≠ 1 und a als Basis (Grundzahl). In der gebräuchlichsten Form sind dabei für den Exponenten x die reellen Zahlen zugelassen. Im Gegensatz zu den Potenzfunktionen, bei denen die Basis die unabhängige Größe (Variable) und der Exponent fest vorgegeben ist, ist bei Exponentialfunktionen der Exponent (auch Hochzahl) des Potenzausdrucks die Variable und die Basis fest vorgegeben. Darauf bezieht sich auch die Namensgebung. Exponentialfunktionen haben in den Naturwissenschaften, z. B. bei der mathematischen Beschreibung von Wachstumsvorgängen, eine herausragende Bedeutung (siehe exponentielles Wachstum).
Als die Exponentialfunktion im engeren Sinne (präziser eigentlich natürliche Exponentialfunktion) bezeichnet man die e-Funktion, also die Exponentialfunktion e^x mit der eulerschen Zahl e = 2,718 281 828 459 … als Basis; gebräuchlich hierfür ist auch die Schreibweise x ↦ exp ( x ). Diese Funktion hat gegenüber den anderen Exponentialfunktionen besondere Eigenschaften. Unter Verwendung des natürlichen Logarithmus lässt sich mit der Gleichung a^x = e^(x ⋅ ln a) jede Exponentialfunktion auf eine solche zur Basis e zurückführen.
Bisweilen unterscheidet man im Deutschen auch zwischen exponentiellen Funktionen (allgemein) und der Exponentialfunktion (zur Basis e).
Lineare Funktion
Als lineare Funktion wird oft (insbesondere in der Schulmathematik) eine Funktion f : R → R der Form f ( x ) = m ⋅ x + n ; m , n e R , also eine Polynomfunktion höchstens ersten Grades, bezeichnet.
Es handelt sich dabei jedoch nicht um eine lineare Abbildung im Sinne der linearen Algebra, sondern um eine affine Abbildung, da die Linearitätsbedingung im Allgemeinen nicht erfüllt ist. Man spricht deswegen auch von einer affin-linearen Funktion. Um eine lineare Abbildung bzw. lineare Funktion im Sinne der linearen Algebra handelt es sich nur im Spezialfall n = 0, also f ( x ) = m x . Solche Funktionen werden auch als homogene lineare Funktion oder Proportionalität bezeichnet. In Anlehnung an diese Bezeichnung wird die Funktion für den Fall n ≠ 0 auch allgemeine lineare Funktion oder linear-inhomogene Funktion genannt. In diesem Artikel wird die häufig verwendete Bezeichnung lineare Funktion beibehalten.
Lineare Funktionen gehören zu den relativ einfachen Funktionen in der Mathematik. Sie sind stetig und differenzierbar. Viele Probleme lassen sich für lineare Funktionen leicht lösen; daher versucht man oft, komplizierte Problemstellungen durch lineare Zusammenhänge zu approximieren.
Logarithmus-Funktion
Als Logarithmus (Plural: Logarithmen; von altgriechisch λόγος lógos, "Verständnis, Lehre, Verhältnis", und ἀριθμός, arithmós, "Zahl") einer Zahl bezeichnet man den Exponenten, mit dem eine vorher festgelegte Zahl, die Basis, potenziert werden muss, um die gegebene Zahl, den Numerus, zu erhalten. Logarithmen sind nur für positive reelle Zahlen definiert, auch die Basis muss positiv sein.
Der Logarithmus einer positiven reellen Zahl x zur Basis b ist also der Wert des Exponenten, wenn x als Potenz zur Basis b dargestellt wird, also diejenige Zahl y, welche die Gleichung b^y = x löst. Man schreibt y = log b ( x ). Das Logarithmieren, d. h. der Übergang von x zu log b ( x ), ist damit eine Umkehroperation des Potenzierens. Die Funktion, die bei gegebener fester Basis b jeder positiven Zahl ihren Logarithmus zuordnet, nennt man Logarithmusfunktion zur Basis b.
Mit Logarithmen lassen sich sehr stark wachsende Zahlenreihen übersichtlich darstellen, da der Logarithmus für große Zahlen viel langsamer steigt als die Zahlen selbst. Wie die Gleichung log b ( x ⋅ y ) = log b ( x ) + log b ( y ) zeigt, kann man durch Logarithmieren eine Multiplikation durch die viel weniger rechenintensive Addition ersetzen. Auch beschreiben Logarithmen auf mathematisch elegante Weise viele technische Prozesse sowie Phänomene der Natur wie etwa das Verhalten einer Halbleiter-Diode, die Spirale eines Schneckenhauses oder die Wahrnehmung unterschiedlicher Lautstärken durch das menschliche Ohr.
Entsprechende mathematische Berechnungen sind bereits aus der Zeit vor Christi Geburt aus Indien überliefert. Der Begriff Logarithmus wurde von John Napier im frühen 17. Jahrhundert geprägt. Napier zu Ehren wird der Natürliche Logarithmus manchmal auch Napierscher Logarithmus oder Neperscher Logarithmus genannt.
Polynom-Funktion
Eine ganzrationale Funktion oder Polynomfunktion ist in der Mathematik eine Funktion, die als Summe von Potenzfunktionen mit natürlichen Exponenten beschrieben werden kann. Somit können solche Funktionen ausschließlich mittels der Operationen Addition, Subtraktion und Multiplikation beschrieben werden. Ganzrationale Funktionen gehören zu den rationalen Funktionen und enthalten ihrerseits als Spezialfälle die linearen und quadratischen Funktionen.
Quadratische Funktion
Eine quadratische Gleichung ist eine Gleichung, die sich in der Form a x^2 + b x + c = 0 mit a ≠ 0 schreiben lässt. Hierbei sind a , b , c Koeffizienten; x ist die Unbekannte. Ist b = 0, spricht man von einer reinquadratischen Gleichung. Die linke Seite dieser Gleichung ist der Term einer quadratischen Funktion (allgemeiner ausgedrückt: ein Polynom zweiten Grades), f ( x ) = a x^2 + b x + c der Funktionsgraph dieser Funktion im Kartesischen Koordinatensystem ist eine Parabel. Geometrisch beschreibt die quadratische Gleichung f ( x ) = 0 die Nullstellen dieser Parabel.
Rationale Funktion
Eine rationale Funktion ist in der Mathematik eine Funktion, die als Quotient zweier Polynomfunktionen darstellbar ist.
Abstrakter kann man für die Koeffizienten a z , … , a 0 , b n , … , b 0 Elemente eines beliebigen Körpers zulassen. Die rationalen Funktionen mit komplexen Koeffizienten gehören zu den meromorphen Funktionen.
Allgemeiner kann man rationale Funktionen in mehreren Variablen sowie rationale Funktionen auf algebraischen Varietäten über beliebigen Körpern betrachten.
Sekans-Funktion
Sekans ist eine trigonometrische Funktionen. Der Sekans wird mit sec ( x ) bezeichnet. Die Funktion hat ihren Namen durch die Definition im Einheitskreis. Die Funktionswerte entsprechen der Länge von Sekantenabschnitten.Im rechtwinkligen Dreieck ist der Sekans das Verhältnis der Hypotenuse zur Ankathete und damit die Kehrwert-Funktion der Kosinusfunktion.
Sinus-Funktion
Die Sinusfunktion ist neben der Cosinus-Funktion eine elementare mathematische Funktion. Vor Tangens und Kotangens, Sekans und Kosekans bildet sie die wichtigste trigonometrischen Funktion. Sinus wird unter anderem in der Geometrie für Dreiecksberechnungen in der ebenen und sphärischen Trigonometrie benötigt. Auch in der Analysis ist sie wichtig.
Wellen wie Schallwellen, Wasserwellen und elektromagnetische Wellen lassen sich als aus Sinuswellen zusammengesetzt beschreiben, sodass die Funktion auch in der Physik als harmonische Schwingung allgegenwärtig sind.
Sinus-hyperbolicus-Funktion
Sinus hyperbolicus ist eine mathematische Hyperbelfunktion, auch Hyperbelsinus genannt; sie trägt das Symbol sinh.
Tangens-Funktion
Tangens ist eine trigonometrische Funktion und spielt in der Mathematik und ihren Anwendungsgebieten eine herausragende Rolle. Der Tangens des Winkels x wird mit tan x bezeichnet. In älterer Literatur findet man auch die Schreibweisen tg x für den Tangens
Die Bezeichnung "Tangens" stammt von dem Mathematiker Thomas Finck (1561–1656), der sie 1583 einführte.
Tangens-hyperbolicus-Funktion
Der Tangens hyperbolicus ist eine Hyperbelfunktion. Man nennt sie auch Hyperbeltangens oder hyperbolischen Tangens.
Wurzelfunktion
In der Mathematik versteht man unter Wurzelziehen oder Radizieren die Bestimmung der Unbekannten x in der Potenz a = x^n
Hierbei ist n eine natürliche Zahl (meist größer als 1) und a ein Element aus einem Körper (häufig eine nichtnegative reelle Zahl). Das Ergebnis des Wurzelziehens bezeichnet man als Wurzel oder Radikal (von lat. radix "Wurzel"). Das Radizieren ist eine Umkehrung des Potenzierens. Im Fall n = 2 spricht man von Quadratwurzeln, bei n = 3 von Kubikwurzeln. Wurzeln werden mit Hilfe des Wurzelzeichens notiert.